Flow-coloring duality

Graphs are one of the simplest sorts of topological spaces. In fact, they’re so simple that topologists don’t usually spend much time studying them. Their homology and homotopy groups are determined purely combinatorially; every connected graph is homotopy equivalent to a wedge sum of circles. Graph theory focuses on stricter combinatorial invariants, usually even stricter than homeomorphism. However, a lot of the algebraic tools that topologists use to study topological spaces have combinatorial properties that encode more than just homotopical information when applied to graphs. Let’s look at the chain complex of a graph, viewed as a simplicial complex.

This is a very simple algebraic object, a complex

$$\cdots \to 0 \to \mathbb{Z}^{|E|} \to \mathbb{Z}^{|V|} \to 0 \to \cdots$$

A flow on $G$ is an element of the kernel of the only nontrivial boundary map of $G$. That is, given an orientation of the edges, it is a choice of an integer $x_e$ for each edge $e$ of $G$ satisfying Kirchoff’s current law: the net flow out of any vertex is zero. This is a very familiar topological object; the kernel of the boundary map is just $H_1(G)$. The fact that we care about the particular combinatorial structure of $G$, however, means that the actual construction of the boundary map is relevant, not just its homology up to isomorphism. In particular, we can look at the way that $H_1(G)$ sits inside $C_1(G) = \mathbb{Z}^{|E|}$. One way to do this is to consider the set of $k$-flows: flows that are less than $k$ in absolute value. By restricting the size of flows, we have gone from a homotopy-invariant object to one depending on the specific combinatorial structure of $G$.

While combinatorial, this quantity still has a sort of topological feel, and topological thinking is still relevant. For example, suppose $G$ is a planar graph with dual $G'$. Every $k$-coloring of $G'$ gives a nowhere-zero $k$-flow on $G$.

To see this, let’s first review the relationship between $G$ and $G'$ from a topological perspective. Since $G$ is a planar graph, it corresponds to a cell decomposition of a simply-connected closed subset of $S^2$.

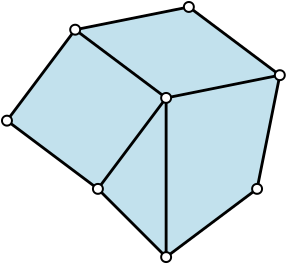
The complement of this subset in $S^2$ is an open disc, so we in fact get a cell decomposition of the sphere. If $G$ is bridge-free, this decomposition is a regular cell decomposition, which means that it has a Poincaré dual.

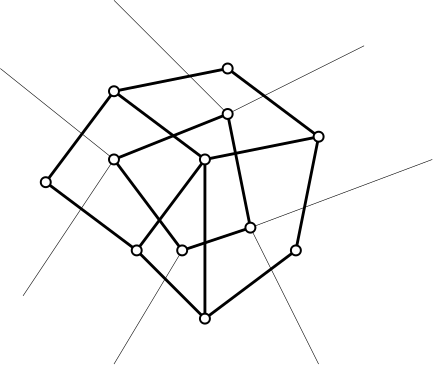
Consider the dual cell complexes $X$ and $X'$, coming from $G$ and $G'$. Both are decompositions of $S^2$, and by construction, we have $C^i(X) = C^{2-i}(X')$. Indeed, the following diagram commutes:

Now, suppose we have a coloring of $G'$, which corresponds to a coloring of the 2-cells of $G$. Integer-valued 0-cochains on $G'$ correspond to colorings, in that if we have a 0-cochain with values in $\{0,\ldots,k-1\}$ whose coboundary vanishes nowhere, it defines a $k$-coloring of $G'$, and vice versa.

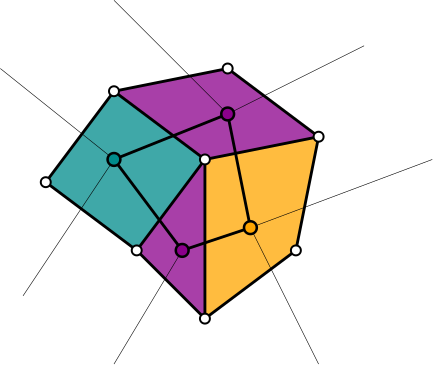
Given a $k$-coloring of $G'$, represented as a 0-cochain $x$, we take $\delta x$, giving a nowhere-vanishing 1-cochain of $G'$. By duality, this corresponds to a 1-chain $y$ of $G$, and we see that $\partial y = 0$ because $\delta^2 x = 0$. Note also that $y$ can never exceed $k-1$ in absolute value, since its value on each edge is the difference of two terms in $\{0,\ldots,k-1\}$. This shows that every $k$-coloring of $G'$ gives a $k$-flow of $G$.

To go from flows to colorings is a bit trickier. A flow $y$ on $G$ is an element of $\ker \partial_1$, since $H_1(S^2) = 0$, $\ker \partial_1 = \text{im } \partial_2$. Thus, every flow on $G$ is the image of a 2-chain on $X$, which corresponds to a 0-cochain $x$ on $X'$. If $y$ is nowhere-zero, $x$ defines a coloring, since it differs over every edge. To get a $k$-coloring, we will use a trick: mod everything out by $k$. A nowhere-zero $k$-flow clearly becomes a nowhere-zero $\mathbb Z/k$-flow. And a 0-cochain valued in $\mathbb Z / k$ whose coboundary vanishes nowhere is clearly equivalent to a $k$-coloring. Since none of the algebra changes when we take the quotient, we see that $x$ defines a $k$-coloring of $G'$.

The flow-coloring duality gives an alternate statement of the four-color theorem: every (bridgeless) planar graph has a nowhere-zero 4-flow. A conjecture that then has the same spirit as the four-color theorem is that every bridgeless graph has a nowhere-zero 5-flow.

This flow-coloring duality extends to higher-dimensional structures. If $X$ and $X'$ are dual cell structures on a compact manifold $M$ of dimension $n$, where $H_{n-1}(M) = 0$, then nowhere-zero $(n-1)$-cycles of $X$ which are everywhere less than $k$ in absolute value correspond to $k$-colorings of the 0-cells of $X'$. I’m not aware of anyone who has studied this, but it seems like an interesting connection between graph theory, topology, and the combinatorics of cell complexes.